티스토리 뷰
InfoDesk/Science
갈릴레이 변환(Galilean Transformation)에서 노출된 고전 역학과 전자기학 사이의 모순에 대한 설명
bizmaker 2024. 10. 26. 06:30[갈릴레이 변환(Galilean Transformation)]
갈릴레이 변환은 고전 역학에서 사용되는 좌표계 변환 방법으로, 다음과 같은 특징을 가진다:
1. 정의
- 서로 다른 관성계 사이의 좌표와 시간을 변환하는 방법
2. 기본 가정
- 시간은 모든 관성계에서 절대적이고 동일하게 흐른다고 가정함.
- 공간의 구조는 모든 관성계에서 동일하게 유지된다고 가정함.
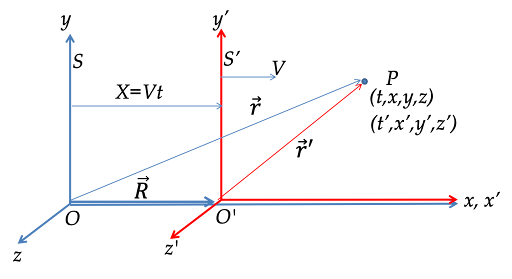
3. 변환 공식
- x' = x - vt
- y' = y
- z' = z
- t' = t
(여기서 v는 두 관성계 사이의 상대 속도, 즉 속도차)
4. 속도 덧셈 법칙
- 갈릴레이 변환에 따르면 속도는 단순히 더해짐.
- 예를 들어, u' = u - v
5. 적용 범위
- 일상적인 속도에서는 잘 적용됨.
- 광속에 가까운 고속에서는 부정확한 결과를 보임.
6. 한계
- 맥스웰 방정식과 같은 전자기 현상을 설명하는 데 실패
- 빛의 속도 불변성을 설명하지 못함.
7. 역사적 의의
- 뉴턴 역학의 기본 원리로 사용됨.
- 특수 상대성 이론이 등장하기 전까지 널리 사용됐음.
8. 대체
- 특수 상대성 이론에서는 갈릴레이 변환 대신 로렌츠 변환을 사용하여 고속에서의 현상을 정확히 설명함.
갈릴레이 변환은 고전 역학의 기본 원리였지만, 현대 물리학에서는 그 한계가 인식되어 특수 상대성 이론의 로렌츠 변환으로 대체됐다.
[고전 역학과 전자기학 사이의 모순]
갈릴레이 변환과 관련하여 고전 역학과 전자기학 사이에는 다음과 같은 모순이 있었던 것으로 조사됐다.
1. 고전 역학의 상대성 원리
- 고전 역학에서는 갈릴레이 변환을 통해 서로 다른 관성계 사이의 물리 법칙이 동일하게 유지된다고 가정함.
- 즉, 뉴턴의 운동 법칙은 모든 관성계에서 동일하게 적용될 것으로 추정
2. 전자기학의 문제
- 맥스웰 방정식으로 표현되는 전자기 법칙은 갈릴레이 변환 하에서도 불변하지 않았음.
- 특히 빛의 속도가 모든 관성계에서 일정하다는 결과는 갈릴레이 변환과 양립할 수 없게 된 상황
3. 에테르 가설의 실패
- 전자기파의 매질로 가정된 에테르에 대한 실험들이 실패하면서, 절대 정지 기준계의 존재가 의문시됨.
4. 로렌츠의 발견
- 로렌츠는 전자의 운동에 맥스웰 방정식을 적용할 때 오류가 발생함을 발견했고,
- 이는 전자의 운동이 갈릴레이 변환을 만족하지 않기 때문이었음.
5. 특수 상대성 이론의 등장
- 아인슈타인은 이러한 모순을 해결하기 위해 갈릴레이 변환 대신 로렌츠 변환을 도입하고,
- 시공간 개념을 재정립하는 특수 상대성 이론을 제안함.
이러한 모순은 결국 고전 역학의 한계를 드러내고, 상대론적 역학의 필요성을 제기하는 계기가 됐다.
특수 상대성 이론은 이 모순을 해결하고 전자기학과 역학을 통합적으로 설명할 수 있는 새로운 패러다임을 제시했다.
[절대 정지 기준계의 필요성]
- 뉴턴이 절대 공간과 절대 시간의 개념을 도입했고, 절대 정지 기준계는 이 절대 공간에 대해 정지해 있는 기준계를 의미하며, 모든 운동을 측정할 수 있는 절대적인 기준점을 제공함.
- 19세기 전자기학에서 빛이 전파되는 매질로 '에테르'(Ether)를 가정했으며, 이 에테르에 대해 정지해 있는 기준계를 절대 정지 기준계로 간주함.
- 모든 물리 법칙이 가장 단순하고 기본적인 형태로 표현될 수 있는 특별한 기준계로 여겨지며 물리 법칙의 보편성을 설명하는 데에 도움이 됨.
- 마이컬슨-몰리 시험도 (에테르의 존재를 확인하기 위한) 지구의 상대 운동을 측정하려는 시도였음.
지구가 에테르를 통과하여 움직인다면 이동 방향에 따라 빛의 속도가 차이가 있을 것으로 예상


반응형
'InfoDesk > Science' 카테고리의 다른 글
| 맥스웰 방정식 관련 이미지 모음 (0) | 2024.10.27 |
|---|---|
| 아인슈타인 논문과 맥스웰 방정식의 변위 전류와의 관계 (2) | 2024.10.27 |
| 맥스웰 방정식과 특수 상대성 이론과의 관계 (2) | 2024.10.25 |
| 맥스웰이 앙페르 법칙에 변위 전류를 추가하게 된 과정 (0) | 2024.10.24 |
| 앙페르-맥스웰 회로 법칙에 대한 설명 (0) | 2024.10.23 |
반응형
250x250
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- 치매방지
- 심심풀이
- image
- 절연형
- Innovations
- 심심풀이치매방지기
- BiliChild
- Innovation&Hurdles
- Video
- 치매
- 티스토리챌린지
- BSC
- 전류
- Innovations&Hurdles
- Hurdles
- 아두이노
- 오블완
- DYOV
- 둎
- ServantClock
- arduino
- 혁신
- 혁신과허들
- bilient
- 배프
- 전압
- 빌리칠드
- 허들
- Decorator
- 빌리언트
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
글 보관함

